BabyEncryption. HackTheBox RE Challenge writeup

Overview

This time we will be focusing on a very simple reverse engineering challenge on HackTheBox called “BabyEncryption”. What made me want to write this post for it was the fact that how being lazy can sometimes (emphasis on ‘sometimes’!) show you new ways to do the same task. So let’s begin.

Write-up

Let’s begin with the simplest and, I think, the intended way. So once we download, check and unzip the files, we see the following python encryption file.

import string
from secret import MSG

def encryption(msg):
    ct = []
    for char in msg:
        ct.append((123 * char + 18) % 256)
    return bytes(ct)

ct = encryption(MSG)
f = open('./msg.enc','w')
f.write(ct.hex())
f.close()

And if we directly run it, we can’t as there is no module name secret. But we can see that we don’t actually need to make the program run if we can simply reverse engineer the code. So if we check the code we find that to encrypt the code, each letter is changed to its ASCII number (most probably), denoted by char here and then the following calculation is done on it.

And once each calculated value is store in the list, it is returned as an immutable bytes object, and this byte value is converted to hex before being saved as the encrypted value in msg.enc.

#1. Let’s solve Math

So if we want to reverse engineer the code, we need to remember what modulus function is. One of the basic definition allows us to write any modulus function as below:

Then we can reverse each calculation with the following pseudo-code:

for i in encoded_msg:
    for some range of m in quotient:
        if ((256*m)+i-18)%123 == 0:
            #append ascii character

And our final code will look like this.

def decryption(hidden):
    arr = list(bytes.fromhex(hidden))
    msg = []
    for i in arr:
        for m in range(100):
            if ((256*m)+i-18)%123 == 0:
                msg.append(chr(((256*m)+i-18)//123))
                break
    print(''.join(msg))


f = open('./msg.enc','r')
hidden = f.readline().strip()
f.close()

decryption(hidden)

#2. Let’s not solve math

Like me, if you want to avoid the brainwork and trade-it off with a bit longer easier work, we need to think of other ways. And one thing we know is that every flag will be in printable characters. So if we just make a dictionary of each possible character we can map the same calculation in the encryption as its key. This way we can replace each value from the numerical array to characters by simply looking up our dictionary!

special = ['!','@','#','$','%','^','&','*','(',')','{','}','.',',','/','\\',' ','_','\n']
dic = {}

# Adding all alphabets
for i,j in zip(range(ord('a'), ord('z')+1), range(ord('A'), ord('Z')+1)):
    mutation_i = (123*i+18)%256; mutation_j = (123*j+18)%256
    dic[mutation_i] = chr(i)
    dic[mutation_j] = chr(j)

# Adding all numbers
for i in range (0,10):
    mutation_i = (123*ord(str(i))+18)%256
    dic[mutation_i] = str(i)

#Adding special characters
for i in special:
    mutation_i = (123*ord(i)+18)%256
    dic[mutation_i] = i

def decryption(msg_encoded):
    msg_bytes = bytes.fromhex(msg_encoded)
    msg_arr = list(msg_bytes)
    msg = []
    for i in msg_arr:
        msg.append(dic[i])
    print(''.join(msg))

f = open('./msg.enc', 'r')
encoded = f.readline().strip()
f.close()

decryption(encoded)

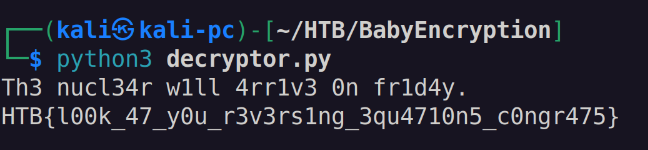
And this gives us the decrypted message as well!